Sortowanie jest podstawową operacją, w której elementy tablicy są ułożone w określonej kolejności w celu zwiększenia możliwości wyszukiwania. W prostych słowach dane są sortowane tak, aby można je było łatwo przeszukiwać.
Wykres porównania
| Podstawa do porównania | Sortowanie przez wstawianie | Wybór Sortuj |
|---|---|---|
| Podstawowy | Dane są sortowane poprzez wstawienie danych do istniejącego posortowanego pliku. | Dane są sortowane poprzez wybranie i umieszczenie kolejnych elementów w posortowanej lokalizacji. |
| Natura | Stabilny | Nietrwały |
| Proces, który należy przestrzegać | Elementy są znane wcześniej, podczas wyszukiwania lokalizacji, aby je umieścić. | Lokalizacja jest znana podczas wyszukiwania elementów. |
| Natychmiastowe dane | Sortowanie wtrąceniowe jest techniką sortowania na żywo, która może zajmować się natychmiastowymi danymi. | Nie może zajmować się bezpośrednimi danymi, musi być obecny na początku. |
| Najlepsza złożoność przypadku | Na) | O (n 2 ) |
Definicja sortowania wstawiania
Sortowanie wstawiania działa poprzez wstawienie zestawu wartości do istniejącego posortowanego pliku. Konstruuje posortowaną tablicę, wstawiając pojedynczy element naraz. Ten proces trwa, dopóki cała tablica nie zostanie posortowana w określonej kolejności. Podstawową koncepcją sortowania wstawiania jest wstawienie każdego elementu do odpowiedniego miejsca na liście końcowej. Metoda sortowania wstawiania oszczędza efektywną ilość pamięci.
Praca z sortowaniem wstawiania
- Używa dwóch zestawów tablic, w których jeden przechowuje posortowane dane i inne na nieposortowanych danych.
- Algorytm sortowania działa, dopóki w zbiorze nieposortowanym nie znajdą się elementy.
- Załóżmy, że w tablicy są elementy liczbowe "n". Początkowo element o indeksie 0 (LB = 0) istnieje w posortowanym zbiorze. Pozostałe elementy znajdują się na nieposortowanej partycji listy.
- Pierwszy element niesortowanej części ma indeks tablicy 1 (jeśli LB = 0).
- Po każdej iteracji wybiera pierwszy element nieposortowanej partycji i wstawia go we właściwe miejsce w posortowanym zestawie.
Zalety sortowania insercji
- Łatwo zaimplementowane i bardzo wydajne w przypadku korzystania z niewielkich zestawów danych.
- Dodatkowe zapotrzebowanie na miejsce pamięci dotyczące sortowania wstawiania jest mniejsze (tj. O (1)).
- Uznaje się ją za technikę sortowania na żywo, ponieważ listę można sortować po otrzymaniu nowych elementów.
- Jest szybszy niż inne algorytmy sortowania.
Przykład:
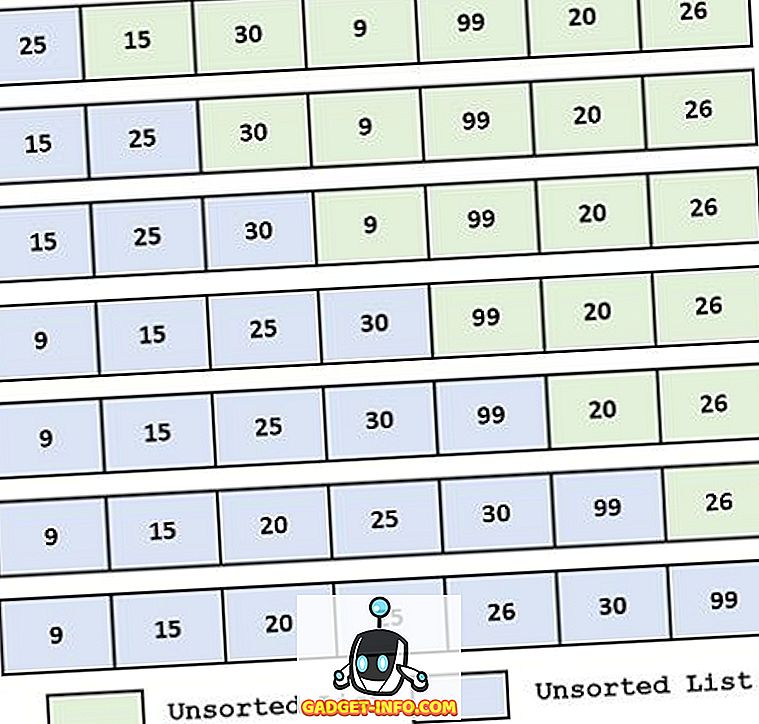
Definicja sortowania
Sortowanie zaznaczeń wykonuje sortowanie, wyszukując minimalną liczbę wartości i umieszczając ją na pierwszej lub ostatniej pozycji zgodnie z kolejnością (rosnącą lub malejącą). Proces wyszukiwania minimalnego klucza i umieszczenia go we właściwej pozycji jest kontynuowany do momentu, aż wszystkie elementy zostaną umieszczone we właściwej pozycji.
Praca z wyborem sortowania
- Załóżmy tablicę ARR z N elementami w pamięci.
- W pierwszym przebiegu szukany jest najmniejszy klucz wraz z jego pozycją, a następnie ARR [POS] zamieniony na ARR [0]. Dlatego ARR [0] jest sortowany.
- W drugim przebiegu ponownie pozycja najmniejszej wartości jest określona w podprzekobieciu elementów N-1. Zamień ARR [POS] na ARR [1].
- W przejściu N-1 wykonuje się ten sam proces, aby posortować liczbę elementów N.
Przykład:
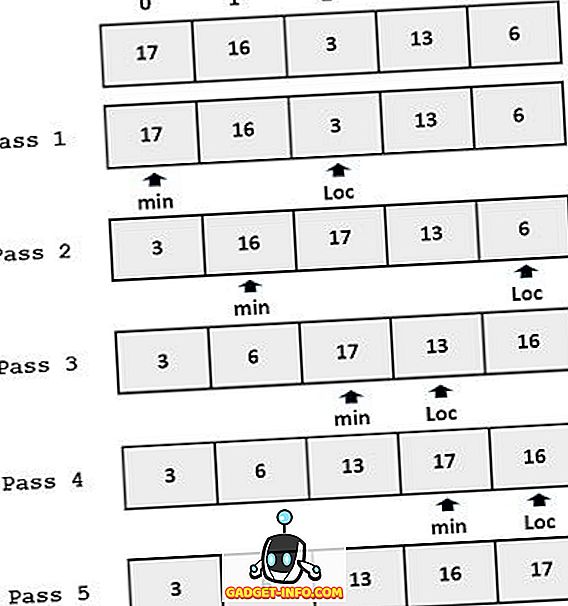
Kluczowe różnice między sortowaniem z wstawianiem i wyborem
- Sortowanie wstawiania zwykle wykonuje operację wstawiania. Przeciwnie, sortowanie selekcji dokonuje wyboru i pozycjonowania wymaganych elementów.
- Sortowanie wsadowe jest stabilne, a sortowanie selekcji nie jest stabilnym algorytmem.
- W algorytmie sortowania wstawiania elementy są wcześniej znane. Natomiast sortowanie selekcji zawiera wcześniej lokalizację.
- Sortowanie metodą wstawiania jest żywą techniką sortowania, w której elementy przychodzące są natychmiast sortowane na liście, a sortowanie według sortowania nie działa dobrze w przypadku danych bezpośrednich.
- Sortowanie z wstawkami ma najlepszy czas działania O (n). W przeciwieństwie do tego, najlepszą złożonością sortowania w przypadku wystąpienia sortowania jest O (n2).
Złożoność sortowania wstawiania
Najlepsza złożoność sortowania wstawek to O (n) razy, tj. Gdy tablica jest wcześniej sortowana. W ten sam sposób, gdy tablica jest sortowana w odwrotnej kolejności, pierwszy element tablicy nieposortowanej należy porównać z każdym elementem w posortowanym zbiorze. Tak więc, w najgorszym przypadku, czas działania sortowania wstawiania jest kwadratowy, tj. O (n2) . W przeciętnym przypadku musi również wykonać minimalne porównania (k-1) / 2. W związku z tym, średni przypadek ma również kwadratowy czas działania O (n2).
Złożoność sortowania selekcji
Jako działanie selekcji sortowanie nie zależy od pierwotnej kolejności elementów w tablicy, więc nie ma dużej różnicy między najlepszym przypadkiem a najgorszym przypadkiem złożoności sortowania.
Sortowanie zaznaczeń wybiera element minimalnej wartości, w procesie selekcji skanowana jest cała liczba elementów "n"; w związku z tym porównania n-1 są dokonywane w pierwszym przebiegu. Następnie elementy są wymieniane. Podobnie w drugim przejściu, aby znaleźć drugi najmniejszy element, musimy skanować elementy spoczynkowe n-1, a proces jest kontynuowany aż do uporządkowania całej tablicy.
Zatem złożoność czasu trwania sortowania selekcji to O (n2) .
= (n-1) + (n-2) + ......... .. + 2 + 1
= n (n-1) / 2 = O (n2)
Wniosek
Wśród obu algorytmów sortowania sortowanie wstawek jest szybkie, wydajne, stabilne, a sortowanie wyboru działa wydajnie tylko w przypadku niewielkiego zestawu elementów lub częściowo wcześniej sortowanej listy. Liczba porównań dokonanych przez sortowanie selekcji jest większa niż wykonanych ruchów, podczas gdy w sortowaniu wstawiania liczba razy, gdy element jest przesuwany lub zamieniany jest większy niż dokonane porównania.