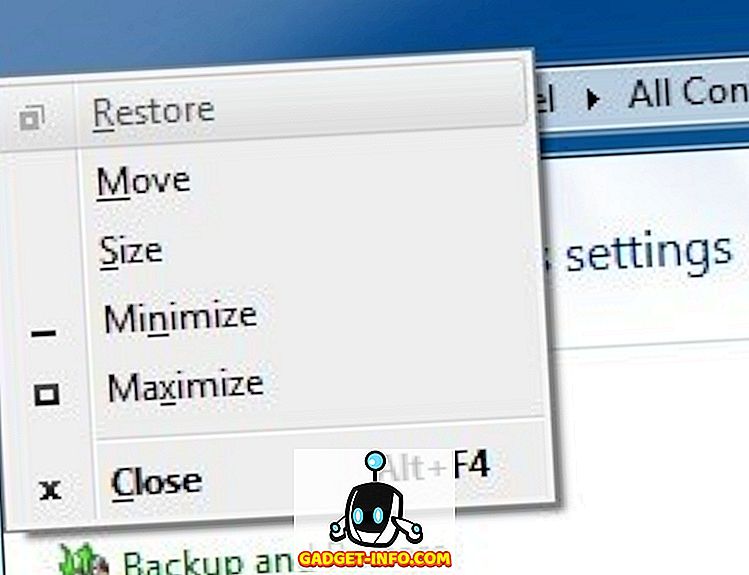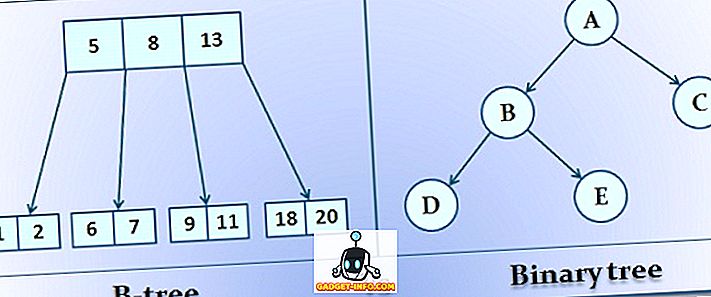
Inną różnicą między drzewem B i drzewem binarnym jest to, że drzewo B musi mieć wszystkie swoje węzły potomne na tym samym poziomie, podczas gdy drzewo binarne nie ma takiego ograniczenia. Drzewo binarne może mieć maksymalnie 2 poddrzewia lub węzły, podczas gdy w drzewie B może mieć M nie poddrzew lub węzłów, gdzie M jest rzędem drzewa B.
Wykres porównania
| Podstawa do porównania | B-drzewo | Drzewo binarne |
|---|---|---|
| Ograniczenie zasadnicze | Węzeł może mieć maksymalną liczbę M węzłów potomnych (gdzie M jest rzędem drzewa). | Węzeł może mieć maksymalnie 2 liczby poddrzew. |
| Używany | Jest używany, gdy dane są przechowywane na dysku. | Jest używany, gdy rekordy i dane są przechowywane w pamięci RAM. |
| Wysokość drzewa | log M N (gdzie m jest rzędem drzewa M-way) | log 2 N |
| Podanie | Struktura danych indeksujących kod w wielu systemach DBMS. | Optymalizacja kodu, kodowanie Huffmana itp. |
Definicja drzewa B-tree
Drzewo B jest zbalansowanym drzewem M-way, znanym również jako drzewo sortowania zrównoważonego. Jest podobny do drzewa wyszukiwania binarnego, w którym węzły są zorganizowane w oparciu o przechodzenie w tryb "inorder". Złożoność przestrzenna drzewa B to O (n). Złożoność czasu wstawiania i usuwania to O (log n).
Są pewne warunki, które muszą być prawdziwe dla drzewa B:
- Wysokość drzewa musi być jak najmniejsza.
- Nad liśćmi drzewa nie powinno być pustych poddrzew.
- Liście drzewa muszą znajdować się na tym samym poziomie.
- Wszystkie węzły powinny mieć najmniejszą liczbę dzieci z wyjątkiem węzłów urlopowych.
Właściwości drzewa B rzędu M
- Każdy węzeł może mieć maksymalną liczbę M dzieci i minimalną liczbę dzieci w M / 2 lub dowolną liczbę od 2 do maksymalnej.
- Każdy węzeł ma jeden klucz mniej niż dzieci z maksymalnymi kluczami M-1.
- Rozmieszczenie kluczy odbywa się w określonej kolejności w obrębie węzłów. Wszystkie klucze w poddrzewie znajdującym się po lewej stronie klucza są poprzednikami klucza, a znajdujące się po prawej stronie klucza nazywane są następcami.
- W momencie wstawienia pełnego węzła drzewo dzieli się na dwie części, a klucz z wartością średnią wstawiany jest do węzła nadrzędnego.
- Operacja scalania ma miejsce po usunięciu węzłów.
Definicja drzewa binarnego
Drzewo binarne to struktura drzewa, która może mieć najwyżej dwa wskaźniki dla węzłów potomnych. Oznacza to, że najwyższy stopień, jaki może mieć węzeł, wynosi 2, a także węzeł zerowy lub jeden stopień.
Istnieją pewne warianty drzewa binarnego, takie jak drzewo binarne, pełne drzewo binarne, rozszerzone drzewo binarne itp.
- Drzewo stricte binarne jest drzewem, w którym każdy węzeł nie będący węzłem końcowym musi pozostawić poddrzewo i poddrzewo prawe.
- Drzewo nazywa się pełnym drzewem binarnym, gdy spełnia warunek posiadania 2 węzłów na każdym poziomie, gdzie i jest poziomem.
- Wątek binarny to drzewo binarne, które składa się z 0 węzłów lub 2 węzłów.
Techniki przekrojowe
Przemieszczenie drzewa jest jedną z najczęstszych operacji wykonywanych na strukturze danych drzewa, w której każdy węzeł odwiedził dokładnie raz w sposób systematyczny.
- Inorder- W tym drzewie przejścia lewe poddrzewo jest odwiedzane rekurencyjnie, a następnie odwiedzany jest węzeł główny i odwiedzane jest ostatnie poddrzewo z prawej strony.
- Preorer- W tym przewrocie drzewa węzeł główny jest odwiedzany najpierw, potem lewy poddrzewo, a na końcu prawy poddrzewo.
- Postorder - Ta technika odwiedza lewe poddrzewo, prawe poddrzewo i ostatni węzeł główny.
Kluczowe różnice między drzewem B i drzewem binarnym
- W drzewie B maksymalna liczba węzłów potomnych, które może mieć węzeł nie-końcowy, to M, gdzie M jest rzędem drzewa B. Z drugiej strony drzewo binarne może mieć co najwyżej dwie podrodziny lub węzły potomne.
- B-drzewo jest używane, gdy dane są przechowywane na dysku, podczas gdy drzewo binarne jest używane, gdy dane są przechowywane w szybkiej pamięci, takiej jak pamięć RAM.
- Kolejnym obszarem zastosowania B-tree jest struktura danych indeksujących kod w DBMS, natomiast drzewo binarne jest wykorzystywane do optymalizacji kodu, kodowania Huffmana itp.
- Maksymalna wysokość drzewa B to log M N (M to kolejność drzew). W związku z tym maksymalna wysokość drzewa binarnego to log 2 N (N to liczba węzłów, a podstawa to 2, ponieważ jest to wartość binarna).
Wniosek
Drzewo B jest używane przez binarne i binarne drzewo wyszukiwania. Głównym powodem tego jest hierarchia pamięci, w której procesor jest podłączony do pamięci podręcznej z kanałami o dużej przepustowości, a procesor jest podłączony do dysku przez kanał o niskiej przepustowości. Drzewo binarne jest używane, gdy rekordy są przechowywane w pamięci RAM (małe i szybkie), a drzewa B są używane, gdy rekordy są przechowywane na dysku (duże i wolne). Zatem użycie drzewa B zamiast drzewa binarnego znacznie skraca czas dostępu z powodu wysokiego współczynnika rozgałęzienia i zmniejszonej wysokości drzewa.