Różnica między permutacją a kombinacją

2019

W matematyce mogłeś usłyszeć pojęcia permutacji i kombinacji razy, ale czy kiedykolwiek wyobrażałeś sobie, że te dwie są różnymi pojęciami? Podstawową różnicą pomiędzy permutacją a kombinacją jest kolejność obiektów, w permutacji kolejność obiektów jest bardzo ważna, tzn. Układ musi być w ustalonej kolejności liczby obiektów, przyjmowanych tylko kilka lub wszystkie naraz.

W związku z tym, w przypadku kombinacji, kolejność nie ma znaczenia. Nie tylko w matematyce, ale także w życiu praktycznym, regularnie sprawdzamy te dwie koncepcje. Chociaż nigdy tego nie zauważamy. Przeczytaj uważnie artykuł, aby dowiedzieć się, jak te dwa pojęcia są różne.

Wykres porównania

Podstawa do porównania	Permutacja	Połączenie
Znaczenie	Permutacja odnosi się do różnych sposobów aranżacji zestawu obiektów w porządku sekwencyjnym.	Kombinacja odnosi się do kilku sposobów wyboru elementów z dużego zestawu obiektów, tak, że ich kolejność nie ma znaczenia.
Zamówienie	Istotnych	Nieistotny
Oznacza	Układ	Wybór
Co to jest?	Zamówione elementy	Nieuporządkowane zestawy
Odpowiedzi	Ile różnych aranżacji można utworzyć z danego zestawu obiektów?	Ile różnych grup można wybrać z większej grupy obiektów?
Pochodzenie	Wiele permutacji z pojedynczej kombinacji.	Pojedyncza kombinacja z jednej permutacji.

Definicja permutacji

Definicja permutacji definiujemy jako różne sposoby aranżacji niektórych lub wszystkich elementów zbioru w określonej kolejności. Zakłada ono wszystkie możliwe układy lub przegrupowania danego zestawu, w rozróżnialny sposób.

Na przykład: Wszystkie możliwe permutacje utworzone za pomocą liter x, y, z -

Biorąc wszystkie trzy naraz, są to: xyz, xzy, yxz, yzx, zxy, zyx.
Biorąc dwie osoby na raz to xy, xz, yx, yz, zx, zy.

Łączna liczba możliwych permutacji n rzeczy, wziętych r na raz, może być obliczona jako:

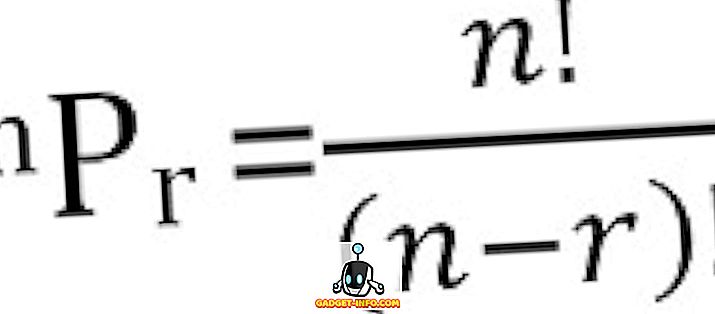
Definicja kombinacji

Kombinacja jest zdefiniowana jako różne sposoby wybierania grupy, przez wzięcie kilku lub wszystkich członków zbioru, bez następującej kolejności.

Na przykład: Wszystkie możliwe kombinacje wybrane z literą m, n, o -

Gdy mają zostać wybrane trzy z trzech liter, jedyną kombinacją jest mno
Gdy mają zostać wybrane dwie z trzech liter, możliwe kombinacje to mn, nie, om.

Łączna liczba możliwych kombinacji n rzeczy, wziętych r na raz, może być obliczona jako:

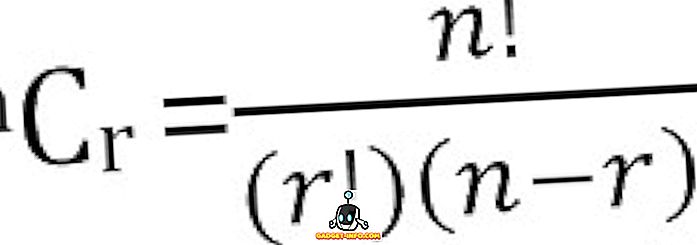
Kluczowe różnice między permutacją a kombinacją

Różnice między permutacją a kombinacją są jasno określone z następujących powodów:

Termin permutacja odnosi się do kilku sposobów aranżacji zestawu obiektów w porządku sekwencyjnym. Kombinacja oznacza kilka sposobów wybierania elementów z dużej puli obiektów, tak, że ich kolejność jest nieistotna.
Podstawowym punktem odróżniającym te dwa pojęcia matematyczne jest porządek, położenie i położenie, tzn. W wymienionych wyżej właściwościach permutacyjnych ma znaczenie, co nie ma znaczenia w przypadku kombinacji.
Permutacja oznacza kilka sposobów aranżacji rzeczy, ludzi, cyfr, alfabetów, kolorów itp. Z drugiej strony, kombinacja wskazuje różne sposoby wybierania pozycji menu, jedzenia, ubrań, przedmiotów itp.
Permutacja to nic innego jak uporządkowana kombinacja, podczas gdy kombinacja implikuje nieuporządkowane zestawy lub parowanie wartości w ramach określonych kryteriów.
Wiele permutacji można uzyskać z pojedynczej kombinacji. I odwrotnie, tylko jedna kombinacja może być uzyskana z jednej permutacji.
Odpowiedzi permutacji Ile różnych aranżacji można utworzyć z danego zestawu obiektów? W przeciwieństwie do kombinacji, która tłumaczy Ile różnych grup można wybrać z większej grupy obiektów?

Przykład

Przypuśćmy, że jest sytuacja, w której musisz znaleźć całkowitą liczbę możliwych próbek dwóch z trzech obiektów A, B, C. W tym pytaniu, po pierwsze, musisz zrozumieć, czy pytanie dotyczy permutacji lub kombinacja i jedynym sposobem, aby to znaleźć, jest sprawdzenie, czy zamówienie jest ważne, czy nie.

Jeśli kolejność jest znacząca, to pytanie dotyczy permutacji, a możliwe próbki to: AB, BA, BC, CB, AC, CA. Gdzie AB różni się od BA, BC różni się od CB, a AC jest innym CA.

Jeśli zamówienie jest nieistotne, pytanie dotyczy kombinacji, a możliwe próbki to AB, BC i CA.

Wniosek

W powyższej dyskusji jasne jest, że permutacja i kombinacja to różne terminy, które są używane w matematyce, statystykach, badaniach i naszym codziennym życiu. Należy pamiętać, że w odniesieniu do tych dwóch koncepcji, dla danego zestawu obiektów, permutacja zawsze będzie wyższa niż kombinacja.