W przeciwieństwie do standardowego odchylenia jest pierwiastkiem kwadratowym z wartości liczbowej uzyskanej podczas obliczania wariancji. Wiele osób kontrastuje z tymi dwoma matematycznymi koncepcjami. Tak więc w tym artykule podjęto próbę wyjaśnienia istotnej różnicy między wariancją a odchyleniem standardowym.
Wykres porównania
| Podstawa do porównania | Zmienność | Odchylenie standardowe |
|---|---|---|
| Znaczenie | Wariancja to wartość liczbowa opisująca zmienność obserwacji od średniej arytmetycznej. | Odchylenie standardowe jest miarą rozproszenia obserwacji w zbiorze danych. |
| Co to jest? | Jest to średnia kwadratowych odchyleń. | Jest to średnie kwadratowe odchylenie. |
| Oznaczone jako | Sigma-kwadrat (σ ^ 2) | Sigma (σ) |
| Wyrażone w | Kwadratowe jednostki | Te same jednostki co wartości w zbiorze danych. |
| Wskazuje | Jak daleko rozrzucone są osoby w grupie. | Ile obserwacji zbioru danych różni się od jego średniej. |
Definicja wariancji
W statystyce wariancję definiuje się jako miarę zmienności, która reprezentuje dystans członków grupy. Dowiaduje się, że średni stopień, w jakim każda obserwacja różni się od średniej. Gdy wariancja zbioru danych jest mała, pokazuje bliskość punktów danych do średniej, podczas gdy większa wartość wariancji oznacza, że obserwacje są bardzo rozproszone wokół średniej arytmetycznej i od siebie nawzajem.
W przypadku niesklasyfikowanych danych :
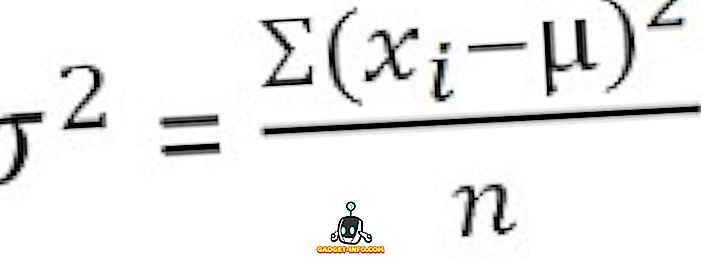
Do zgrupowanego rozkładu częstotliwości :
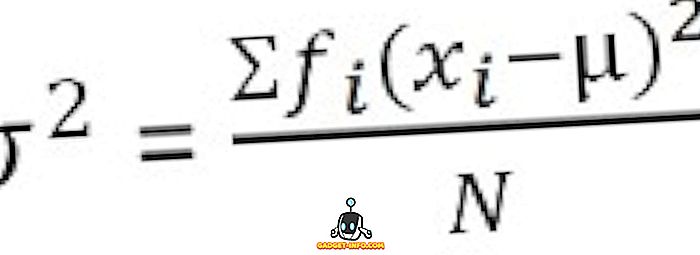
Definicja odchylenia standardowego
Odchylenie standardowe jest miarą, która określa ilościowo dyspersję obserwacji w zbiorze danych. Niskie odchylenie standardowe jest wskaźnikiem bliskości wyników do średniej arytmetycznej i oznacza wysokie odchylenie standardowe; wyniki są rozproszone w większym zakresie wartości.
W przypadku niesklasyfikowanych danych :

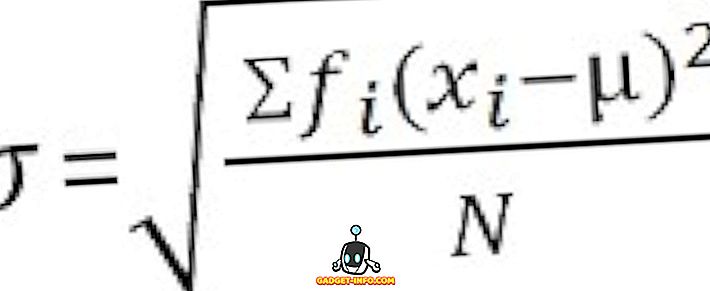
Kluczowe różnice między wariancją a odchyleniem standardowym
Różnicę między odchyleniem standardowym a odchyleniem można wyraźnie wytłumaczyć z następujących przyczyn:
- Wariancja to wartość liczbowa opisująca zmienność obserwacji od średniej arytmetycznej. Odchylenie standardowe jest miarą rozproszenia obserwacji w zbiorze danych.
- Wariancja to nic innego jak średnią kwadratowych odchyleń. Z drugiej strony odchylenie standardowe jest odchyleniem kwadratowym średniej kwadratowej.
- Wariancja jest oznaczona jako sigma-kwadrat (σ2), natomiast odchylenie standardowe jest oznaczone jako sigma (σ).
- Wariancja jest wyrażona w jednostkach kwadratowych, które są zwykle większe niż wartości w danym zbiorze danych. W przeciwieństwie do odchylenia standardowego wyrażonego w tych samych jednostkach, co wartości w zbiorze danych.
- Odchylenie mierzy stopień rozłożenia jednostek w grupie. Odwrotnie, odchylenie standardowe mierzy, ile obserwacji zbioru danych różni się od średniej.
Ilustracja
Oceny uzyskane przez ucznia w pięciu przedmiotach wynoszą odpowiednio 60, 75, 46, 58 i 80. Musisz znaleźć odchylenie standardowe i wariancję.
Przede wszystkim musisz dowiedzieć się, co to znaczy

Tak więc średnia (średnia) wynosi 63, 8
Teraz obliczyć wariancję
| X | ZA | (xA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3, 8 | 14, 44 |
| 75 | 63.8 | 11.2 | 125, 44 |
| 46 | 63.8 | -17.8 | 316, 84 |
| 58 | 63.8 | 5.8 | 33, 64 |
| 80 | 63.8 | 16.2 | 262, 44 |
Gdzie, X = Obserwacje
A = średnia arytmetyczna
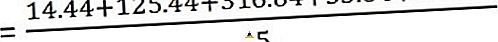
Odchylenie standardowe to -

Podobieństwa
- Zarówno wariancja, jak i odchylenie standardowe są zawsze dodatnie.
- Jeśli wszystkie obserwacje w zbiorze danych są identyczne, wówczas odchylenie standardowe i wariancja będą zerowe.
Wniosek
Te dwa są podstawowymi pojęciami statystycznymi, które odgrywają istotną rolę w różnych sektorach. Odchylenie standardowe jest korzystniejsze od średniej, ponieważ jest wyrażane w tych samych jednostkach, co w przypadku pomiarów, natomiast wariancja wyrażana jest w jednostkach większych niż dany zestaw danych.